都立高校入試<数学>の分析と攻略法
都立高校入試の数学は、一部の学校を除いて同じ「共通問題」を使用します。
各設問の内容や正答率がほぼ決まっているため、目標点数に合わせて対策がしやすいです。
特に大問1は基礎的な計算問題が中心で、確実に得点を狙える部分です。
大問2以降は関数や図形などの難易度が上がりますが、パターンを押さえれば対応可能です。
過去問(表過去問・裏過去問)を使って、しっかりと基礎を固めることが高得点への近道です。
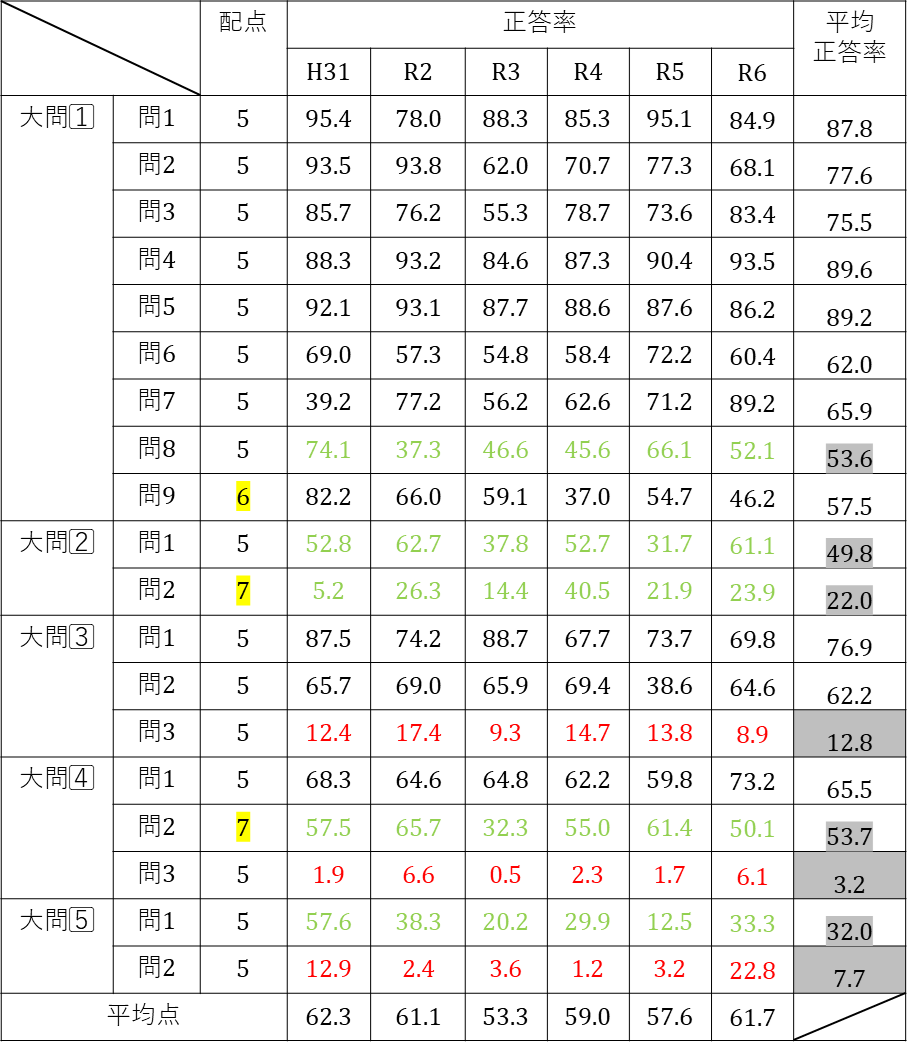
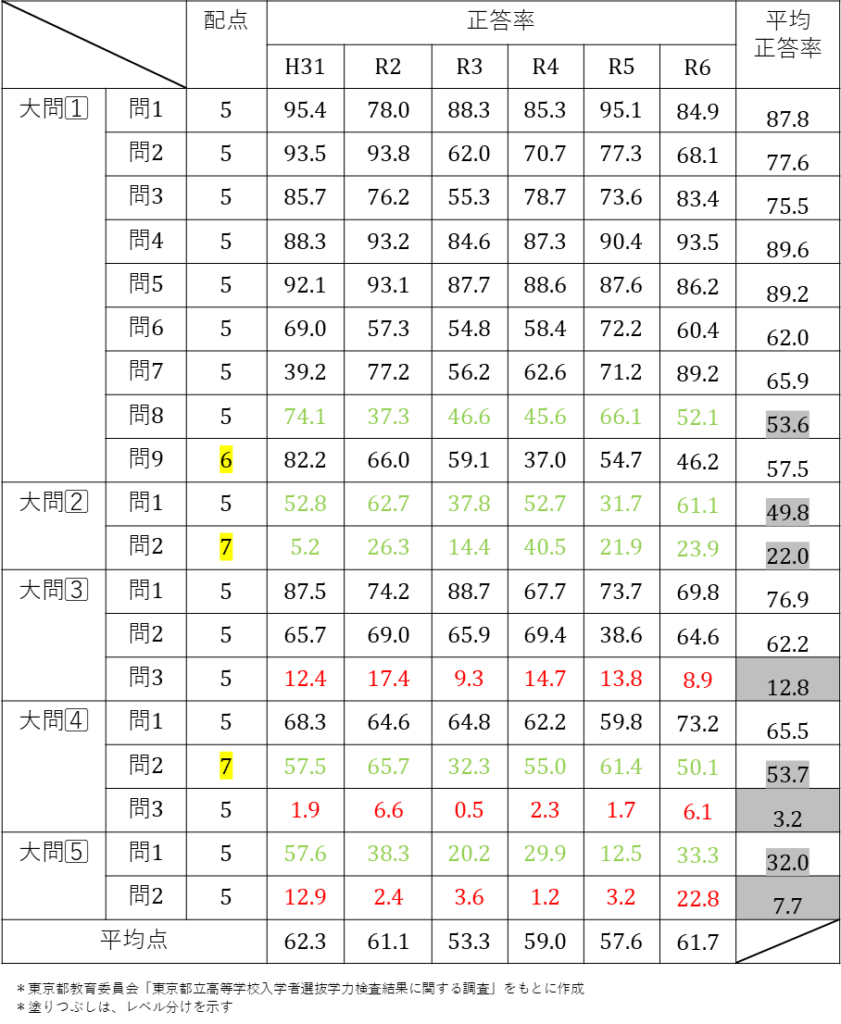
配点と正答率
基礎固めを最優先(大問1)
基礎的な計算問題を確実に得点できるように練習しましょう。目標は完璧に解けるようにすること。
目標点数に応じた問題選択(大問2以降)
難易度が上がるので、自分のレベルに合った問題を選んで取り組みます。高得点を目指す場合は、難問にも挑戦する意識を持ちましょう。
過去問の活用
過去問を通して出題パターンを把握し、頻出問題に備えましょう。表過去問・裏過去問の両方を活用して、総合的な対策を行います。
令和6年度の傾向
- 全体 :例年通りの難易度。
- 大問1:箱ひげ図に関する易しい問題。
- 大問2:図をイメージしやすい内容。
- 大問3:直線QRの式を求める問題がポイント。
- 大問4:問3は、例年に比べて易しい問題。
- 大問5:問3は、例年に比べて易しい問題。
令和7年度の予想
- 大問1:場合の数や確率に注意。
- 大問2:整数に関する問題が出題される可能性。
- 大問3:一次関数を重点的に対策。
- 大問4:円に関する問題に注意。
- 大問5:直方体に関する問題が出題されると予想。
補足
これらの予想は、対策の優先順位を決めるための参考です。全体の復習と合わせて取り組みましょう。
<大問1>の対策
前期・一次募集と後期・二次募集の問題

大問1の単元
| 問1 | 正負の数 |
| 問2 | 文字と式 |
| 問3 | 平方根 |
| 問4 | 一次方程式 |
| 問5 | 連立方程式 |
| 問6 | 二次方程式 |
| 問7 問8 | 変域、データの整理と分析、確率、角度、弧の長さ |
| 問9 | 作図 |
大問1の対策
まずは、大問1で満点を目指しましょう。
高得点を狙うためには、見直しに時間を使い、計算ミスを防ぐことが大切です。
特に計算部分に重点を置き、時間を計りながら練習すると効果的です。
問9では作図問題が出題されます。作図技法には「垂線」「垂直二等分線」「角の二等分線」の3つがあります。それぞれの基本的な違いを理解することで、適切な技法を選べるようになります。
ポイント
作図に用いる技法は、主な技法は「垂線」「垂直二等分線」「角の二等分線」の3つなのに、間違えてしまいます。それは、基本のパターンの違いを理解できていないからです。
垂線 ・・・点と直線の関係を示す
垂直二等分線・・・点と点の関係を示す
角の二等分線・・・直線と直線の関係を示す
これらを理解していると、問題の設定条件に合う技法を選択できるようになり、作図が得意になります。
裏過去問でしっかりと練習しましょう。
<大問2>の対策
大問2では、数理的な考察や推論を正確に表現する力が求められます。
毎年形式が少し異なるため、苦手な方も多いですが、今年度は比較的易しい問題で、正答率は42.5%でした。
都立数学では、証明と作図を除き、各問題5点です。問題の難易度を見極め、どの問題から取りかかるかを判断する力も重要です。
前期・一次募集と後期・二次募集の問題

大問2の単元
| 問1 | 式による表現 |
| 問2 | 式の証明 |
大問2の対策
問題文から条件を読み取り立式する演習、推論の過程を根拠に基づき相手に分かりやすく伝える演習が必要です。過去問の模範解答を何回も書写(再現)してください。
なお、規則性の問題には市販教材が少ないため、「裏過去問」を使ってしっかり演習しましょう。
<大問3>の対策
大問1から大問3の問2までは、正答率も50%を超えているので、安定した点数(60点以上)を確保することが大切です。
大問3では、主に関数(y=a𝑥+bのグラフ、y= a𝑥2のグラフ)の問題が出題されます。
前期・一次募集と後期・二次募集の問題

大問3の単元
| 問1 | 座標/変域 |
| 問2 | 直線の式 |
| 問3 | 条件を満たす座標 |
大問3の対策
問1
座標を求める問題や変域を求める問題が出されます。
問2
直線の式を求める問題が頻出です。直線上の2点の座標がわかると、あとは、直線の式を求める手順に従って、計算するだけです。
問3
例年、点Pの座標を求める問題が多く、正答率は低いですが、解法パターンをマスターすれば対応可能です。3つのステップに分けて解くことで、難問も攻略できるようになります。
(1)点Pの座標を設定する。
(2)与えられた条件に係る図形の座標を点Pの座標を用いて表す。
(3)与えられた条件を満たす等式を作る。
正答率が低い主な理由は、ひと工夫しないと解けない問題がほとんどだからです。
その点に着目できると、本番でも解ける可能性が高まるでしょう。
<大問4>の対策
大問4では、平面図形を題材にした問題が出題されます。
前期・一次募集と後期・二次募集の問題

大問4の単元
| 問1 | 角の大きさと文字式 |
| 問2 | 図形の証明 |
| 問3 | 線分、線分比、面積、面積比 |
大問4の対策
問1
平行線、三角形、平行四辺形、円といった図形の性質を用いて角度を求めます。
問2
問題文から条件を読み取り、三角形の合同条件や相似条件を特定します。過去問の模範解答を何回も書写(再現)して証明方法を覚えましょう。
問3
正答率が10%以下の難問が出やすいため、偏差値60以下の高校を志望する場合は他の問題に優先的に取り組むのが良いかもしれません。
例年、与えられた図から解答を導くために必要となる相似な図形を探す力、利用する力が問われています。
つまり、等しい角を見つけるために、三角形の外角の定理、平行線の性質(平行線の錯角や同位角)、二等辺三角形の性質、平行四辺形の性質、円の性質(円周角の定理)、特別な三角形(辺の比や角度が特定される三角形)は、頻出するので、瞬時に思いつくように学習しておきましょう。
基礎的な知識を組み合わせる演習を裏過去問で重ねることで、本番の問題にも対応できるようになるでしょう。
<大問5>の対策
大問5では、空間図形における角度や立体の体積を求める問題が出題されます。
前期・一次募集と後期・二次募集の問題

大問5の単元
| 問1 | 線分の長さ、角度、直線の位置関係、面積 |
| 問2 | 立体の体積 |
大問5の対策
問1
求める線分や角度が含まれる平面を特定し、図形を明確にしましょう。
問2
正答率が低いため、他の問題を優先するのも一つの方法です。ただし、解法パターンをマスターすれば得点源となります。
立体の体積は、3つのステップに分けて求めます。
(1)立体の体積(すい体)は、「1/3×底面積×高さ」より求める。
(2)底面積を含む図形を図示し、底面積を求める。
(3)高さを含む平面を図示し、高さを求める。
このステップを理解することで、体積の問題も得点源となります。
ポイント
正答率が低い主な理由は、高さを含む平面図形を想起できないからです。
求める立体の高さは、求める立体の底面が、元の立体の底面に垂直である場合、元の立体を横に切る断面に現れ、求める立体の底面が、元の立体の底面に垂直でない場合、元の立体を縦に切る断面に現れることがほとんどです。
なお、求める立体の底面は、問題文に示されています。例えば、立体P-ADEBの体積を求める場合は、底面は、面ADEBです。